C 排序算法
冒泡排序
冒泡排序(英语:Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。
过程演示:

实例
#include <stdio.h>
// 函数声明
void bubble_sort(int arr[], int len);
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
bubble_sort(arr, len); // 调用冒泡排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
// 冒泡排序函数
void bubble_sort(int arr[], int len) {
for (int i = 0; i < len - 1; i++) {
for (int j = 0; j < len - 1 - i; j++) {
// 交换元素位置
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
过程演示:


实例
#include <stdio.h>
// 函数声明
void selection_sort(int a[], int len);
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
selection_sort(arr, len); // 调用选择排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
// 选择排序函数
void selection_sort(int a[], int len) {
for (int i = 0; i < len - 1; i++) {
int min = i; // 记录最小值的位置,第一个元素默认最小
for (int j = i + 1; j < len; j++) {
if (a[j] < a[min]) { // 找到目前最小值
min = j; // 记录最小值的位置
}
}
// 交换两个变量
if (min != i) {
int temp = a[min];
a[min] = a[i];
a[i] = temp;
}
}
}
/*
// 自定义交换函数
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
*/
插入排序
插入排序(英语:Insertion Sort)是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到 {\displaystyle O(1)} {\displaystyle O(1)}的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后
挪位,为最新元素提供插入空间。过程演示:

实例
#include <stdio.h>
// 函数声明
void insertion_sort(int arr[], int len);
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
insertion_sort(arr, len); // 调用插入排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
// 插入排序函数
void insertion_sort(int arr[], int len) {
for (int i = 1; i < len; i++) {
int temp = arr[i]; // 当前待插入的元素
int j = i;
// 向右移动大于temp的元素
while (j > 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = temp; // 插入元素到正确位置
}
}
希尔排序
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
过程演示:

实例
#include <stdio.h>
// 函数声明
void shell_sort(int arr[], int len);
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
shell_sort(arr, len); // 调用希尔排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
// 希尔排序函数
void shell_sort(int arr[], int len) {
// 计算初始间隔
for (int gap = len / 2; gap > 0; gap /= 2) {
// 对每个间隔进行插入排序
for (int i = gap; i < len; i++) {
int temp = arr[i]; // 当前待插入的元素
int j = i;
// 移动大于temp的元素
while (j >= gap && arr[j - gap] > temp) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp; // 插入元素到正确位置
}
}
}
归并排序
把数据分为两段,从两段中逐个选最小的元素移入新数据段的末尾。
可从上到下或从下到上进行。
过程演示:

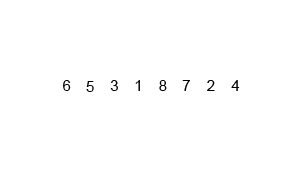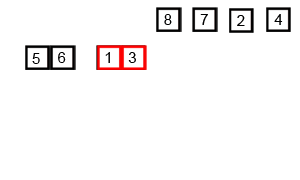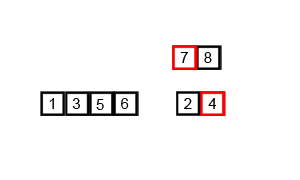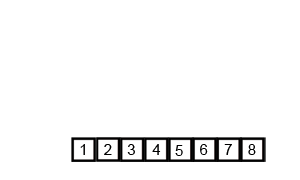
迭代法
#include <stdio.h>
#include <stdlib.h>
// 函数声明
int min(int x, int y);
void merge_sort(int arr[], int len);
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
merge_sort(arr, len); // 调用归并排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
// 返回两个数中的最小值
int min(int x, int y) {
return x < y ? x : y;
}
// 归并排序函数
void merge_sort(int arr[], int len) {
int* a = arr;
int* b = (int*) malloc(len * sizeof(int));
if (b == NULL) { // 检查内存分配是否成功
fprintf(stderr, "Memory allocation failed\n");
exit(EXIT_FAILURE);
}
for (int seg = 1; seg < len; seg += seg) {
for (int start = 0; start < len; start += seg + seg) {
int low = start;
int mid = min(start + seg, len);
int high = min(start + seg + seg, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
// 合并两个子数组
while (start1 < end1 && start2 < end2) {
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
}
while (start1 < end1) {
b[k++] = a[start1++];
}
while (start2 < end2) {
b[k++] = a[start2++];
}
}
// 交换数组指针
int* temp = a;
a = b;
b = temp;
}
// 如果a和arr不相同,则将a的内容复制回arr
if (a != arr) {
for (int i = 0; i < len; i++) {
b[i] = a[i];
}
b = a;
}
free(b); // 释放内存
}
递归法
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// 函数声明
void merge_sort_recursive(int arr[], int reg[], int start, int end);
void merge_sort(int arr[], const int len);
int main() {
int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
merge_sort(arr, len); // 调用归并排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
// 递归实现归并排序
void merge_sort_recursive(int arr[], int reg[], int start, int end) {
if (start >= end)
return;
int mid = start + (end - start) / 2;
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
merge_sort_recursive(arr, reg, start1, end1);
merge_sort_recursive(arr, reg, start2, end2);
int k = start;
while (start1 <= end1 && start2 <= end2) {
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
}
while (start1 <= end1) {
reg[k++] = arr[start1++];
}
while (start2 <= end2) {
reg[k++] = arr[start2++];
}
// 使用memcpy进行数组复制,提高效率
memcpy(arr + start, reg + start, (end - start + 1) * sizeof(int));
}
// 归并排序入口函数
void merge_sort(int arr[], const int len) {
int* reg = (int*)malloc(len * sizeof(int));
if (reg == NULL) { // 检查内存分配是否成功
fprintf(stderr, "Memory allocation failed\n");
exit(EXIT_FAILURE);
}
merge_sort_recursive(arr, reg, 0, len - 1);
free(reg); // 释放内存
}
快速排序
在区间中随机挑选一个元素作基准,将小于基准的元素放在基准之前,大于基准的元素放在基准之后,再分别对小数区与大数区进行排序。
过程演示:

迭代法
#include <stdio.h>
// 范围结构体
typedef struct _Range {
int start, end;
} Range;
// 创建新的范围
Range new_Range(int s, int e) {
Range r;
r.start = s;
r.end = e;
return r;
}
// 交换两个整数
void swap(int *x, int *y) {
int t = *x;
*x = *y;
*y = t;
}
// 快速排序函数
void quick_sort(int arr[], const int len) {
if (len <= 0)
return; // 避免 len 等于负值时引发段错误(Segment Fault)
Range r[len];
int p = 0;
r[p++] = new_Range(0, len - 1);
while (p > 0) {
Range range = r[--p];
if (range.start >= range.end)
continue;
int mid = arr[(range.start + range.end) / 2]; // 选取中间点为基准点
int left = range.start, right = range.end;
do {
while (arr[left] < mid) ++left; // 检测基准点左侧是否符合要求
while (arr[right] > mid) --right; // 检测基准点右侧是否符合要求
if (left <= right) {
swap(&arr[left], &arr[right]);
left++;
right--; // 移动指针以继续
}
} while (left <= right);
if (range.start < right) r[p++] = new_Range(range.start, right);
if (range.end > left) r[p++] = new_Range(left, range.end);
}
}
int main() {
int arr[] = {22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70};
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
quick_sort(arr, len); // 调用快速排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}
递归法
#include <stdio.h>
// 交换两个整数
void swap(int *x, int *y) {
int t = *x;
*x = *y;
*y = t;
}
// 递归实现快速排序
void quick_sort_recursive(int arr[], int start, int end) {
if (start >= end)
return;
int mid = arr[end];
int left = start, right = end - 1;
while (left < right) {
while (left < right && arr[left] < mid)
left++;
while (left < right && arr[right] >= mid)
right--;
swap(&arr[left], &arr[right]);
}
if (arr[left] >= arr[end])
swap(&arr[left], &arr[end]);
else
left++;
quick_sort_recursive(arr, start, left - 1);
quick_sort_recursive(arr, left + 1, end);
}
// 快速排序入口函数
void quick_sort(int arr[], int len) {
quick_sort_recursive(arr, 0, len - 1);
}
int main() {
int arr[] = {22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70};
int len = sizeof(arr) / sizeof(arr[0]); // 计算数组长度
quick_sort(arr, len); // 调用快速排序函数
// 打印排序后的数组
for (int i = 0; i < len; i++) {
printf("%d ", arr[i]);
}
return 0;
}


唐瓷
mrz***[email protected]
1. 希尔排序缩小递增量必须是要互质的。
2. 快速排序可以不用交换中间值。
以下代码仅供参考:
void Array_Map_Sort_Quickly_Extrem(int* Array, int start, int end) { int i=start; int j=end; int Pivot = Array[end]; if(start<end) { while(i<j) { while(i<j &&Array[i]<=Pivot) i++;//Note: i choose the end as parameter Array[j]=Array[i]; while(i<j &&Array[j]>=Pivot) j--; Array[i]=Array[j]; } Array[i]= Pivot; } else return; Array_Map_Sort_Quickly_Extrem(Array,start,i-1); Array_Map_Sort_Quickly_Extrem(Array,i+1,end); }唐瓷
mrz***[email protected]
学神之女
dff***[email protected]
有种排序叫做猴子排序(Bogo Monkey):
如果数据稍多的话,几乎是不可能排序好的。
排序代码:
#include <time.h> #include <stdlib.h> #include <stdbool.h> void swap(int* x, int* y){ //交换 int temporary = *x; *x = *y; *y = temporary; } void randomize(int arr[], int length){ //打乱数组 for(int i = 0; i < length; i++){ srand(time(NULL)+i);//引入i增加随机性 if(rand()%2) swap(&arr[i],&arr[i+1]); } //printf("!");//记录打乱次数 } bool isSorted(int arr[], int length){ for(int i = 0; i < length; i++) if(arr[i]>=arr[i+1]) return false; return true; } void bogoSort(int array[], int length){ while(!isSorted(array,length)) randomize(array,length); }Demo:
#include <stdio.h> int main(){ int numbers[] = {20,9,233,0,-23,7,1,666,4,345,63,45,2,45}; bogoSort(numbers,14);//也可以改成更小 for(int i = 0; i < 14; i++) printf("%d,",numbers[i]); }学神之女
dff***[email protected]
varible
185***[email protected]
冒泡排序是一种稳定的排序方式!
选择排序是一种不稳定的排序方式!
所谓稳定,就是指排完序后序列的各个元素的下标不会改变,如:冒泡排序
第零趟:2,3,2,1
第一趟:2 2 1 3
2:2 1 2 3
3: 1 2 2 3
排完之后,加粗的2还在前面。
所谓不稳定,恰恰相反,如:选择排序
第零趟:2 3 2 1
第一趟:1 3 2 2
第二趟:1 2 3 2
3:1 2 2 3
排完之后,加粗的2到后面去了。
稳定性非常重要!
varible
185***[email protected]